thomasbe86
Well-known member
I am trying to find the best fit for a potentiometer within my circuit, but really, in simulation I only ever use A and B taper... I never really understood how the others work...
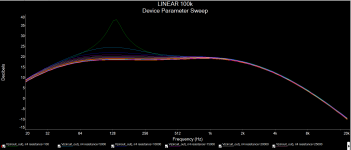
Here are the graphs with both tapers; I am greedy and looking for a more precise transistion on the early course of the pot, like "extra" log...
Basically; the lower the resistance, the louder the hump at 130Hz
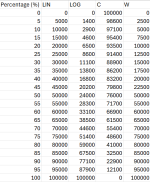
Can anyone give me a clue on what each value would look like for C and W tapers? table at the end is what ChatGPT told me they behave like for a 100k pot, not sure this sounds correct...



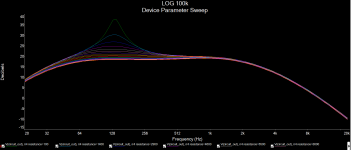
Here are the graphs with both tapers; I am greedy and looking for a more precise transistion on the early course of the pot, like "extra" log...
Basically; the lower the resistance, the louder the hump at 130Hz
Can anyone give me a clue on what each value would look like for C and W tapers? table at the end is what ChatGPT told me they behave like for a 100k pot, not sure this sounds correct...