Opamps for Dummies - part 5

[Chuck D. Bones]

It's been a minute. This time around, we'll discuss gain, bandwidth and slew-rate.

A typical opamp contains four functional blocks. The input stage, the gain stage, the output stage and the bias network. The input stage senses the difference between the the + and - inputs, amplifies that difference and sends it to the gain stage. The gain stage makes most of the voltage gain and drives the output stage. The output stage is typically a push-pull emitter-follower. Its purpose is to provide a low-impedance output and the ability to drive a feedback network and the next stage or device. The voltage gain of an emitter follower is close to unity, but there is a lot of current gain in the output stage. The bias network provides the various DC voltages and currents need to bias each stage. Opamps are intended to have a negative feedback loop around them which controls the DC operating point, gain and frequency response and minimizes distortion. With no feedback, the DC voltage gain of an opamp is very high, typically from 100,000x to a million or more. This is called the "open-loop gain." When we close a feedback loop around an opamp, then we get what's called "closed-loop gain." More on that in part 6. Opamps are designed to be stable under a wide variety of conditions and that is accomplished with something called "compensation." Basically, compensation reduces the open-loop gain at higher frequencies to prevent oscillation when feedback is applied.

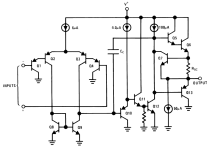
The schematic below shows the innards of an LM358 opamp. I chose that one because it is simple. The opamps we use contain a similar, albeit more complicated, circuit. Q1-Q4, Q8 & Q9 are the input stage. Q2 & Q3 form a differential amplifier. For small signals, the collector currents in Q2 & Q3 are proportional to the voltage difference between Q2-B & Q3-B. Q1 & Q4 are emitter-followers which increase the input impedance and reduce the DC input current. Q8 & Q9 form a "current mirror." What a current mirror does is it makes the current flowing into Q9 equal to the current flowing in to Q8. This converts the differential signal that opamp's input to a single-ended voltage at Q10's base. The diff amp & current mirror provide voltage gain in the neighborhood of 300x. Q10-Q12 form the voltage gain stage. Q10 & Q11 are emitter followers which prevent Q12 from loading the diff amp stage. Q12 is loaded by a current source (that circle with an arrow inside marked 100uA). This part of the circuit has a voltage gain around 1,000x. Notice Cc, that's the compensation capacitor. It's wrapped around the voltage gain stage and causes the gain to drop as frequency increases. Q5-Q7 & Q13 are the output stage. Q5, Q6 & Q13 are emitter-followers in a push-pull arrangement. Q7 provides short-circuit protection by killing the drive to Q5 if the current in Rsc gets too high.


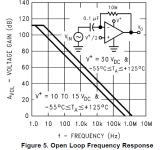
This next chart shows the open-loop gain vs. frequency. We're interested in the left-hand curve because it more-or-less reflects the conditions found in a guitar pedal. Notice that at DC, the gain is around 110dB (approx 300,000x). Also notice that the gain starts dropping off around 2Hz. The LM358's open-loop gain hits unity somewhere around 500KHz. This is not a good opamp to use in a high-gain application because at 10KHz, the open-loop gain is down to 34dB (50x). The term "bandwidth" describes the maximum frequencies we can pass thru a circuit. If we want 40dB gain with an LM358, the bandwidth is limited to 6 or 7KHz.



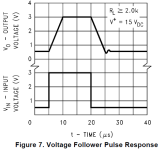
Last thing we will talk about is slew rate. Slew rate describes how quickly the output voltage can change and it is expressed in V/us. Some opamp datasheets specify slew rate, others do not. The LM358 datasheet does not specify a guaranteed slew-rate, but it does give us a clue of what to expect. This next chart shows the opamp slewing as fast as it can. The output voltage changes by 2.5V in 5us. That makes the slew rate 2.5/5 = 0.5V/us. What controls the slew rate? Two things: the maximum current capabilities of Q3 & Q9, and the value of Cc. When the output is slewing, Cc is being charged or discharged by Q3 or Q9. Their current is limited to 6uA by the current source above Q2 & Q3. In other words, 6uA is the most current Q3 or Q9 can put into, or take out of the bottom end of Cc. Making Cc smaller speeds up the slew rate, but at the risk of high-freq oscillations. See that squiggle in the trace around 25us? That's ringing and if it got much worse, the opamp could break into oscillation. Most opamps are internally compensated and we get what we get as far as slew rate and bandwidth go. A few opamps, like the LM308 and CA3130, have external compensation that lets us tailor the slew rate & bandwidth.



Next time: closed-loop gain, feedback and more about compensation.

 

[BuddytheReow]

Forgive my ignorance, but why should we care about slew rate when choosing an opamp or designing a circuit? I tend to only hear this “buzz word” when people are arguing about an authentic Rat (lm308) on other forums. Or will this be answered in part 6? I’ll need to reread the above a few dozen more times to fully sink in….

 

[Chuck D. Bones]

Good question and I will answer it in detail in part 6. Hopefully, you won't have to wait another year for that. I did discuss the LM308 in a few articles. People talk about slew-rate as it pertains to the LM308's tone, but I think they are barking up the wrong tree. In my opinion, what makes the LM308 sound as good as it does is down to three factors:
1. They clip symmetrically or nearly so when driven to saturation.
2. They have limited bandwidth which means when they are driven to saturation, they are not capable of generating a bunch of high-order harmonics.
3. They recover gracefully from saturation. This is hard to describe, but some opamps make some ugly waveforms as they come out of saturation. Again, the result is the LM308 does not produce nasty high-order harmonics.

 

[YourGuitarist]

In the next installment, I'd like to know more about gain bandwidth products if possible. From your explanation here, it seems that while bandwidth constraints from the GBP and slew rate limiting have similar end results, they have separate causes. Slew rate is rather intuitive but why gain and bandwidth are at odds is a mystery to me. It's cool though because that pattern shows up elsewhere such as loudspeaker design and oscillator/bandpass design.

 

[Chuck D. Bones]

Gain-Bandwidth product is simple. It's the frequency at which the open-loop gain goes to unity (0dB). In the plot above, that frequency is about 500KHz on the lower curve. What GBW tells us is how much gain you can have for a given bandwidth, or how much bandwidth you can have for a given gain. with most opamps, the open-loop gain vs. freq is a straight line on a log/log plot, so every point on that curve (above the 2Hz corner freq) has the same GBW.

Cc and the 6uA current source control both GBW and slew rate. Cc reduces the open-loop gain as frequency goes up. At a high enough frequency, the open-loop gain drops to unity. As I wrote above, the 6uA current source and Cc's value limit how quickly Cc can charge or discharge. The definition of a capacitor is it is a device whose voltage rate of change (how fast it charges or discharges) is equal to i / C where i is the charging or discharging current and C is the capacitance. If we put one amp into a one farad capacitor, its voltage will change at a rate of one volt per second. If we have a 12pF capacitor and charge it with 6uA, then the voltage changes at a rate of 0.5V/us. That means that Cc in the LM358 is around 12pF.

 

[Sturdag Lagernathy]

...but I think they are barking up the wrong tree.

Yes! Thank you!
Can't wait for pt. 6!

 

[jesuscrisp]

Why choose the LM358 which is hardly if ever used in pedals for anything else than LFO if I may ask?
Also disagree that it isn't great for high gain, depending on what sort of high gain you're after. Other than some of its nasty crossover clipping behavior, I thought it sounds great for sludgy, dirty gain tones.

 

[Chuck D. Bones]

I think you're missing the point.
I explained why I chose the LM358. I could have picked a TL072 or a 741 for that matter and the circuit description would have been twice as long, harder to follow and would not have told you any more about compensation, slew rate or bandwidth. If it isn't clear why I said what I said about using an LM358 in a high gain circuit, then maybe you and I have different definitions for the term "high gain." It might be more clear when I get to part 6.