GPT-5 Circuit Analysis

R

rossbalch

Active member
Hey folks, thought I would give GPT-5 a go at some (?simple) circuit analysis. I'm not a circuit wizz myself so not sure how well it did but here is the analysis.

You said:

how is the frequency range determined in this circuit

2d53e340-f073-4dde-a8d5-f949a9d54041.png

ChatGPT said:

Great question — this is a midrange active bandpass filter (very similar to the Fender/Marshall tone stack mid control with a sweepable center frequency). Let’s break it down:

​
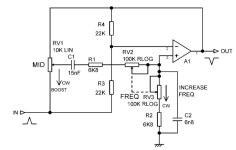
1. What kind of filter is this?

  • The op-amp (A1) is wired as an active bandpass / peaking EQ stage.
  • The resistors (R1, R2, R3, R4) and capacitors (C1, C2) form the frequency-selective network.
  • RV2 and RV3 are dual ganged "frequency" pots (reverse-log) that sweep the effective RC ratio, shifting the center frequency.
​
2. Center frequency formula

The “frequency” section (R1, R2, RV2, RV3, C1, C2) behaves like a state-variable filter.

The approximate center frequency fcfc is set by the resistor–capacitor product:

fc≈12πReqCfc≈2πReqC1

  • CC is mostly defined by C1 (15 nF) and C2 (6.8 nF).
  • ReqReq is the effective resistance from RV2, RV3, R1, and R2 as the pot sweeps.
  • As you turn the frequency knob, the resistance path between the capacitors and ground changes → shifting the “resonant” point.
​
3. Range determination

  • Capacitors C1 and C2 set the overall scaling. Larger C → lower frequency range; smaller C → higher.
  • Pots RV2 & RV3 (100k RLOG each) set how far the resistive divider can swing → determines the sweep width (span).
  • Resistors R1 and R2 (6.8k each) prevent the frequency from going all the way to DC or ultrasonic → they set the limits of the sweep.
So:

  • Lower limit of the sweep is roughly when RV2, RV3 are at maximum resistance (so ReqReq is large).
  • Upper limit is when RV2, RV3 are at minimum (so ReqReq is small).
  • The actual band of frequencies is roughly:
fmin∼12π(Rmax)C,fmax∼12π(Rmin)Cfmin∼2π(Rmax)C1,fmax∼2π(Rmin)C1

where Rmin/maxRmin/max are set by the pot values plus the fixed resistors.

​
4. The “MID” control (RV1)

  • RV1 adjusts the gain (boost/cut) of the mid band.
  • At center frequency, it either attenuates or boosts relative to the bypassed signal.
​
✅ In summary:
The frequency range is determined by C1, C2, R1, R2, and the sweep of RV2 & RV3. Increasing C1 or C2 lowers the entire sweep range; increasing R1/R2 also lowers it. The dual-ganged frequency pots slide the effective RC ratio, sweeping the band center from low mids to high mids.

​
Do you want me to actually calculate the approximate sweep range (in Hz) for the given values (15nF, 6.8nF, 6.8kΩ, 100kΩ pots)?
Click to expand...

You said:

yes please

ChatGPT said:

Here’s a ballpark sweep for the parts shown (C1 = 15 nF, C2 = 6.8 nF, R1 = R2 = 6.8 kΩ, RV2 = RV3 = 100 kΩ R-log).
Treat the “FREQ” pair as varying the effective resistance seen by the caps from roughly Rmin ≈ 6.8 kΩ (pots near CW) to Rmax ≈ ~100–107 kΩ (pots near CCW). Using the usual f≈12πRCf≈2πRC1:

  • Using C1 = 15 nF:
    fmax⁡≈12π(6.8 k)(15 nF)≈1.56 kHzfmax≈2π(6.8k)(15nF)1≈1.56kHz
    fmin⁡≈12π(106.8 k)(15 nF)≈100 Hzfmin≈2π(106.8k)(15nF)1≈100Hz
  • Using C2 = 6.8 nF:
    fmax⁡≈12π(6.8 k)(6.8 nF)≈3.44 kHzfmax≈2π(6.8k)(6.8nF)1≈3.44kHz
    fmin⁡≈12π(106.8 k)(6.8 nF)≈219 Hzfmin≈2π(106.8k)(6.8nF)1≈219Hz
Because the mid-peaking network uses both caps, the practical center-frequency sweep ends up roughly in the ~150 Hz to ~3.4 kHz range, with most of the musical action ~200 Hz–2 kHz.

How to shift the range:

  • Double C1 and C2 → halves the whole sweep.
  • Halve them → doubles the sweep.
  • R1/R2 larger → lowers both ends; smaller → raises both ends.
Click to expand...
You said:

I would like to create two controls, one with roughly 200hz to 1khz, and another with roughly 500hz to 5khz

ChatGPT said:

Awesome—here are concrete parts that will give you two sweepable mids close to your targets. I’m using the same simple f≈12πReqCf≈2πReqC1 read of this network, with the FREQ pots (dual-ganged 100 k RLOG) sweeping ReqReq from about Rmax≈106.8 kΩRmax≈106.8kΩ down to RminRmin set by the fixed resistors (R1, R2).

Low-mid control ≈ 200 Hz → 1.06 kHz

  • Keep C1 = 15 nF
  • Keep C2 = 6.8 nF
  • Change R1 = R2 = 22 kΩ (sets Rmin≈22 kΩRmin≈22kΩ)
  • Dual 100 k RLOG FREQ pots as shown
Result (calc):

  • fmin≈12π⋅106.8k⋅6.8nF≈219  Hzfmin≈2π⋅106.8k⋅6.8nF1≈219Hz
  • fmax≈12π⋅22k⋅6.8nF≈1.06  kHzfmax≈2π⋅22k⋅6.8nF1≈1.06kHz
High-mid control ≈ 500 Hz → 5 kHz

  • Set C1 ≈ 6.8 nF (keeps the C1:C2 ratio similar to stock)
  • Set C2 ≈ 3.0 nF (use 3.0 nF; 3.3 nF gives ~450 Hz–4.8 kHz)
  • Set R1 = R2 = 10.7 kΩ (10 k + 680 Ω in series is perfect)
  • Dual 100 k RLOG FREQ pots as shown
Result (calc, with C2 = 3.0 nF):

  • fmin≈12π⋅106.8k⋅3.0nF≈497  Hzfmin≈2π⋅106.8k⋅3.0nF1≈497Hz
  • fmax≈12π⋅10.68k⋅3.0nF≈4.97  kHzfmax≈2π⋅10.68k⋅3.0nF1≈4.97kHz
How to build it

  • Either duplicate the whole mid stage (two op-amp bands, each with its own FREQ and MID/boost control), or use a switch (rotary or DPDT/3PDT) to swap the R1/R2/C1/C2 set between the low-mid and high-mid values above.
  • Keeping the C1:C2 ratio roughly the same between modes preserves the “Q/shape” feel; R3/R4 can stay as in your drawing unless you want a different Q/boost amount.
If you want, I can sketch a quick switch matrix so you can flip between LOW MID and HIGH MID on one board.
Click to expand...
 
tegendemuur said:
Isn't this exactly why it's such a horrible tool? That you have to ask other humans how well your barebones effort / high output did?
Click to expand...

I don't think it's black and white really? I reject the idea it was barebones effort. I came across this circuit because I've been reading Douglas Self's Small Signal Audio. While the circuit is briefly discussed, the critical components that select the frequency range were not explained. I have a day job, and I want to enjoy my hobby. So if an LLM can save me some precious time, and teach me some stuff along the way, then that's more time I have to design and build.

It's not like I'm asking it to design the entire circuit. I'm still making critical decisions, I just want to understand how these circuit blocks work.

In this case, the frequency range of the circuit was noted in the book, I had GPT analyse the frequencies to see how close it got, and actually it nailed it. This gave me more confidence in the rest of the answer.
thomasbe86 said:
I think he was just happy to share what he tried with the community..
Click to expand...
So yeah. I guess I thought this would be useful info for the community. Cause GPT-4 certainly did not really get this stuff right a lot of the time, but if GPT-5 is more reliable there is the possibility it could be a somewhat useful too for little time savers like this.
 
rossbalch said:
So yeah. I guess I thought this would be useful info for the community. Cause GPT-4 certainly did not really get this stuff right a lot of the time, but if GPT-5 is more reliable there is the possibility it could be a somewhat useful too for little time savers like this.
Click to expand...
And appreciate you sharing, anything related to AI seems to trigger kind of a bit of heat lately in the DIY world. Especially in communities where we actually mostly use the work of others, bit of a conundrum. Keep up the research!
 
rossbalch said:
It's not like I'm asking it to design the entire circuit. I'm still making critical decisions, I just want to understand how these circuit blocks work.
Click to expand...

I drop opamp stages onto ChatGPT and ask it to calculate/plot the frequency response somewhat regularly.

Sure I could do it myself, but it takes seconds, why would I not use the more efficient tool?

It's not a 100% success, it sometimes misinterprets the circuit that I've provided, but so do I... :ROFLMAO:
 
thomasbe86 said:
anything related to AI seems to trigger kind of a bit of heat lately in the DIY world.
Click to expand...
Really it seems to be the case almost anywhere. I get it- water supplies for communities get depleted or ruined so that someone can generate slop for ruining online communities.

So I think any thread about it is going to get meta.

Also personally, as soon as I notice some text is AI generated, I have a strong aversion to read any further. It’s probably because I can’t tolerate when someone is bullshitting me. Bullshit is a fundamental attribute of an LLM.

That said, LLMs do have utility. I use them everyday at work to speed up software development. They do boring things like write mapping functions or boilerplate code.

To OP’s credit, sometimes I use it for pedal building. I have worked out successful mods with it before. But I will also make it verify the work, provide schematics, info from data sheets. And you kind of need to catch some bad assumptions it works off (aka bullshit). It will often fail abysmally at switching logic.
 
I do understand the aversion something like AI triggers and I do understand there is a lot more at stake. What I don't get is how hateful and rude people get towards users rather than aiming at the companies who provide these. I find it an easy way to clear one's concsious but not really helping a cause. I do use it for probably more than I should, sometimes I find myself opening the app for random stuff and "chatting" with it like it's my buddy.. tough to draw the line when something new comes up like this, but yeah when I see something I don't enjoy in a community, I move on to something I like, don't really get the point of raining on someone's parade to unleash my negative opinions about what they do
 
As for the written part with all the – everywhere, it does'nt bother me one bit as long as it reflects what the author means. I use it a lot at work as well to translate emails and reply in languages I don't really master (German ugh) and I usually quickly read and translate back to make sure it's on point and just send as is, not gonna spend time removing the em – and all to pretend I am not using it.. I am not a native English speaker either but I am not half bad anymore, my partner uses it to write most of our news post and all on the website or socials, it is just faster unless you then take the time to make it sound like it is not AI generated :LOL:
 
@thomasbe86 Note my location and a certain company nearby that's essential for LMMs, and semi-conductors in general. Being part of that company, and being force-fed how great "AI" is, because the hype needs to go on, you could say I get triggered easily. It's quite hard for me to not get defensive on this topic. I'm truly sorry if what I said came across as rude. That's not my intention. But there's a whole lot of things wrong with LLMs that I cannot see a users posting his use case here, from how on the other hand it's sending people who are not doing great mentally, into the deep end. Among many other things.

Kinda like people buying non-snouted dogs. We should get rid of them because of their inherent health issues, but people keep buying them because those born need care / love to; they become part of the problem. So yeah, I'll probably refrain from clicking on topics like this, for everyone's sake. 😅
 
Definitely shades of grey.

I'm okay with the AI Tech when used as a tool, such as in this case or another good example is how RWL uses AI to generate pedal art and then further tweak it as needed to get to the desired result... (and it looks great!)

rwl

Thread 'Pharmacist: "This Bird Hasn't Flown Overdrive"'

This is a report on my build of the PPCB Pharmacist. I built this pedal as a Christmas present for my girlfriend, who's a huge Beatles fan. It's a nice overdrive.

birdflown_front.jpg

Inspiration
I was thinking about what bird would best fit the Beatles. Of course there's Blackbird, Blue Jay Way, And Your Bird Can Sing. I had other plans for blackbird-related pedals, and the other songs are not among my top Beatles songs. But I love Norwegian Wood. I thought it would be funny to do a Penguin pedal, for a bird that can't fly. As I mentioned, my girlfriend is a fan of the Beatles, and likes...
  • Like
  • Love
  • This ROCKS!

My own forays into pedal art were rife with too many fingers or an object blending into a body part — other random errors; I've since grown a distaste for the photo-semi-realism of most AI-gen-art.



AI works well as an aid while maintaining critical thinking, but blindly following it is fraught with peril — possibly the most popular (or at least most cloned) compressor circuit is NOT an optical topology:

Feral Feline

Thread 'Best Opto-coupler for Dyana-Ross compressor?'

As a bass-player, I've avoided Dyana-Ross style compressors because I've always read that the Dyana-Rosie style compressors lose low-end;
I've often parroted and perpetuated that sentiment, but actually I've never built one!

So instead of being a stupid mynah-mimic and relaying hearsay and repeating what I've read online, I thought I'd build one and learn for myself first-hand whether it loses lows or not.
Having no experience with Dyana-Ross, I did a Google search to find out what type of compressor it is and what I'll need to build one...

DYNACOMP OPTO-mised 2025-06-02 .png
Subsequent searching... well, it...
  • Haha

If it can't get that right, what other misguided notions is that AI giving people?


Here's another somewhat recent blatant error:

BEST PHASER FOR BASS GOOGLE AI.png
"OTA-based phasers, like those found in the MXR Phase 90..." — Well, at least Gurgles Eh-Aye got the Keeley correct.
I basically quickly scroll down past the "AI Overview" so that I can find more trusted sources of info.


I have to say I don't like the automated responses that give a little pat on the ego — "Good Question!..." It's a f#$%^&* bot, it doesn't know a good from bad question. I'd prefer a neutral response, such as "It's xyz, which broken down into its constituent parts reveals x and y and z" instead of "Awesome question! It's XYZ. Let's break it down..." — Really? "Awesome"? "LET's..."


What if the question isn't about phasers, what if it's about something more important?

PARENT: "My 4-year-old child just made a salad out of HEMLOCK and ate it all while on our picnic, what should we do?"
TRUST-e AI: "Excellent! Such behaviour is an important part of Child Development. Encourage your child to try making other delicious dishes."


The sad part is that the same people that believe in the genuine aforementioned Google-AI produced errors, ehr, info, are likely the ones that get their news-of-the-world from the same source and then vehemently adhere to their opinions formed upon the deluge of misinformation the Web disseminates.


Use it, by all means, but proceed doing so cautiously.
 
Feral Feline said:
AI works well as an aid while maintaining critical thinking, but blindly following it is fraught with peril — possibly the most popular (or at least most cloned) compressor circuit is NOT an optical topology:
Click to expand...

Absolutely, that's why I started with asking it a question I already knew the answer to. A sort of safety question to inform your confidence level in the rest of the answer.

I also think what your post shows is not all LLMs have the same "quality" of output. Gemini, is a lot worse than GPT, I guess because they don't want to allot as much computing power to the summaries as a more deliberate query like you would with ChatGPT.
 
There is one task that I have found that ChatGPT can do better than any other option.... identify SMD components by their manufacturer markings.

If I tell it the marking code, package style, and what type of circuit I think it might be in (audio amplifier, power supply, etc) it has correctly identified everything I have thrown at it, and pointed me to the datasheet. As @JTEX knows from his recent Rockman foray, this is a pretty big deal. :ROFLMAO:
 
You can set up a template for LLMs - that way it will stick within those guardrails initially.

Half the problem is it is not taught the basics, the fundamentals, of circuit design but instead cross references and those designs it encounters more in the training data it learns is correct, except when they're not. It's probably better to create a specialised LLM for electronics design and then get an LLM to interact with it in a more human way.. however the mainstream LLMs are simply 'throw the internet at it'.

I did the Oxford uni 6 week programme (gotta love 17hour+ study and writing assignments each week) on AI. It's also provides a good framework to see past all the BS hype (coupled with almost 30 years in the software biz).
 
You must log in or register to reply here.
Back
Top